![Planolândia (Abbott 2002 [1884]) Planolândia (Abbott 2002 [1884])](https://www.laspa.slg.br/wp-content/uploads/2021/04/planolandia_capa-716x1024.jpg)
Planolândia (Abbott 2002 [1884])
ABBOTT, Edwin A. 2002. Planolândia: um romance de muitas dimensões. (trad. Leila de S. Mendes) São Paulo: Conrad. [1884]
Obs: a paginação indicada se refere a um arquivo pdf [entre colchetes a paginação da edição impressa].


TEXTO INICIAL:
Ó, dia e noite, como isto é maravilhosamente estranho. […] Que vergonha, como eu enquadro desvairadamente meu discurso! (Abbott 2002:4 [11])
Aos
Habitantes do ESPAÇO EM GERAL
E a H. C. [Howard Candler, matemático amigo de Abbott, professor na mesma escola em que lecionava também Charles Howard Hinton] em PARTICULAR
Esta Obra é Dedicada
Por um Humilde Nativo de Planolândia
Na Esperança de que
Da mesma forma que ele foi Iniciado nos Mistérios
Das TRÊS Dimensões
Tendo sido anteriormente versado
Em APENAS DUAS
Os Cidadãos daquela Região Celeste
Possam aspirar cada vez mais
Aos segredos das QUATRO, CINCO OU ATÉ MESMO SEIS Dimensões
Dessa forma contribuindo
para o Engrandecimento DA IMAGINAÇÃO
E o possível Desenvolvimento
Do raríssimo e excelente Dom da MODÉSTIA
Entre as Raças Superiores
Da HUMANIDADE TRIDIMENSIONAL (Abbott 2002:5 [12])
PREFÁCIO À SEGUNDA EDIÇÃO REVISTA, 1884, PELO EDITOR
É verdade que de fato temos em Planolândia uma terceira dimensão não percebida, denominada ‘altura’, da mesma forma vocês têm em Espaçolândia uma quarta dimensão não percebida, que no momento ainda não tem nome, mas que eu vou chamar de ‘altura extra’. Assim como não conseguimos tomar conhecimento de nossa ‘altura’, vocês não conseguem tomar conhecimento de sua ‘altura extra’. Mesmo eu – que estive na Espaçolândia e tive o privilégio de compreender por 24 horas o significado de ‘altura’ – hoje não consigo compreendê-la, nem percebê-la por meio da visão ou por qualquer processo racional. Posso apreendê-la tão-somente por meio da fé. […] A razão é óbvia. Dimensão implica direção, medida, o mais e o menos. Ora, todas as nossas linhas são igual e infinitesimalmente espessas (ou altas, como quiser); conseqüentemente, não há nada nelas que sugira a nossas mentes o conceito daquela dimensão. Nenhum ‘micrômetro de precisão’ – como foi sugerido por um açodado crítico de Espaçolândia – seria de qualquer utilidade para nós, porque não saberíamos o que medir, nem em qual direção. Quando vemos uma linha, vemos algo que é extenso e brilhante; o brilho, assim como a extensão, é necessário a existência de uma linha. Se o brilho desaparece, a linha se extingue. Por isso, todos os meus amigos de Planolândia – com os quais eu falo sobre a dimensão não percebida que é de alguma forma visível em uma linha – dizem: ‘Ah, você quer dizer brilho‘. E quando eu respondo: ‘Não, estou falando de uma dimensão de fato’, eles imediatamente retrucam: ‘Então a mensure, ou nos diga em que direção ela se estende’. E isso me silencia, porque não posso fazer nenhuma das duas coisas. (Abbott 2002:6-7 [14])
Suponha que uma pessoa da quarta dimensão, decidida a visitá-lo, dissesse: ‘Todas as vezes que você abre os olhos, você vê um plano (que tem duas dimensões) e infere um sólido (que tem três), mas na realidade você também vê (embora não perceba) uma quarta dimensão, que não é cor, brilho nem qualquer coisa do tipo, e, sim, uma dimensão de verdade, embora eu não possa lhe mostrar sua direção, nem você possa mensurá-la‘. O que você diria a tal visitante? Você mandaria prendê-lo? Bem, essa é a minha sina […]. Ai de nós, a cegueira e o preconceito são traços comuns à humanidade em todas as dimensões! Pontos, linhas, quadrados, cubos, cubos extras – somos todos passíveis dos mesmos erros, todos igualmente escravos de nossos respectivos preconceitos dimensionais (Abbott 2002:7 [15])
PARTE I – Este mundo
Seja paciente, porque o mundo é largo e vasto. (Abbott 2002:8 [17])
1. Da natureza de Planolândia
Veja, por exemplo, um triângulo eqüilátero – que representa entre nós um comerciante da classe média. A figura 1 representa o comerciante como você o veria quando estivesse inclinado sobre ele; as figuras 2 e 3 representam o comerciante como você o veria com os olhos mais próximos do nível da mesa, ou quase ao nível dela; e, se seus olhos estivessem no nível da mesa (e é dessa forma que o vemos em Planolândia), tudo o que você veria seria uma linha reta. (Abbott 2002:9 [20])

Se nosso amigo se aproxima de nós, vemos sua linha ficar maior. Se ele se afasta, fica menor, mas ainda assim ele se parece com uma linha reta. Seja ele triângulo, quadrado, pentágono, hexágono, círculo. O que seja, ele parece ser uma linha reta e nada além disso. (Abbott 2002:10 [20-1])
2. Do clima e das casas de Planolândia
Como no seu caso, também temos quatro pontos cardeais: norte, sul, leste, oeste. (Abbott 2002:10 [22])
Segundo uma Lei da nossa Natureza, há uma atração constante para o sul, e, embora nos climas temperados ela seja muito fraca […], o efeito restritivo dessa atração é suficiente para servir de bússola na maioria dos lugares da nossa terra. Além disso, a chuva (que cai a intervalos fixos), que sempre vem do norte, é uma ajuda adicional, e nas cidades temos a orientação das casas, que obviamente têm as paredes laterais em sua maior parte na direção norte-sul, de modo que os telhados as protejam da chuva que vem do norte. (Abbott 2002:10 [22])
Antigamente, uma questão interessante e muito investigada por nossos eruditos era: “Qual é a origem da luz?“, e a resposta foi repetidamente buscada, tendo como único resultado a lotação de nossos manicômios com os candidatos a descobridores. Em conseqüência, depois de tentativas infrutíferas de reprimir tais investigações indiretamente, tornando-as sujeitas a pesado imposto, o Legislativo, em uma época comparativamente recente, proibiu-as totalmente. Eu – ai de mim, somente eu em Planolândia – sei hoje muitíssimo bem a verdadeira solução desse misterioso problema, mas meu conhecimento não pode ser tornado inteligível para nenhum de meus compatriotas. (Abbott 2002:11 [23])
A forma mais comum de construção de casas é a de cinco lados ou pentagonal, como na figura abaixo. Os dois lados voltados para o norte, RO e OF, formam o telhado, que em sua maioria não tem portas. No lado leste há uma pequena porta para as mulheres; no lado oeste, uma porta bem maior para os homens; o lado sul ou chão em geral não tem porta. (Abbott 2002:11 [23])
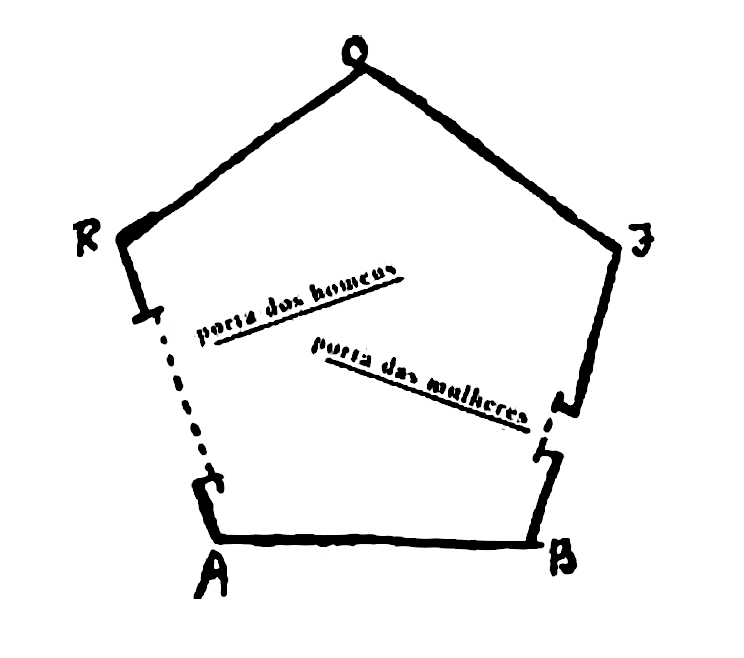
Não são permitidas casas quadradas e triangulares pelo seguinte motivo: como os ângulos de um quadrado (e ainda mais os ângulos de um triângulo eqüilátero) são muito mais pontudos do que os de um pentágono, e como as linhas dos objetos inanimados (tais como casas) são mais indistintas do que as linhas dos homens e das mulheres, segue-se que o perigo de que as pontas de uma casa quadrada ou triangular possam ferir seriamente um viajante desatencioso ou talvez distraído que vá de encontro a elas não é pequeno. E, já no século onze de nossa era, casas triangulares eram universalmente proibidas por lei, sendo as únicas exceções fortificações, paióis de pólvora, quartéis e outros prédios públicos, dos quais a população em geral não deve se aproximar sem circunspeção. Nessa época, casas quadradas ainda eram permitidas, embora desencorajadas por um imposto específico. Mas, uns três séculos depois, a justiça decidiu que em todas as cidades com população superior a 10 mil, o ângulo do pentágono seria o menor ângulo permitido nas casas consistentemente com a segurança pública. O bom senso da comunidade apoiou os esforços do Legislativo, e hoje, mesmo no campo, a construção pentagonal suplantou todas as outras. Atualmente, só em algum distrito agrícola distante e atrasado é que um antiquário poderá ainda descobrir uma casa quadrada. (Abbott 2002:11-2 [24])
3. Sobre os habitantes de Planolândia
Nossas mulheres são linhas retas. […] Nossos soldados e as classes mais baixas de trabalhadores são triângulos com dois lados iguais […] e uma base ou terceiro lado tão curto […] que eles formam nos vértices um ângulo muito agudo e perigoso. Na verdade, quando suas bases são do tipo mais degradado (não passando de alguns milímetros de tamanho), eles mal podem ser distinguidos das linhas retas, ou mulheres, de tão pontudos que são seus vértices. […] Nossa classe média consiste de triângulos eqüiláteros, ou de lados iguais. […] Nossos profissionais e cavalheiros são quadrados (a cuja classe eu pertenço) e figuras de cinco lados, ou pentágonos. […] Acima deles, temos a nobreza, que possui vários graus, começando com as figuras de seis lados, ou hexágonos, e daí em diante aumentando o número de lados até que recebem o título honorífico de polígono, ou figuras de muitos lados. Finalmente, quando o número de lados fica tão grande, e os próprios lados tão pequenos, que a figura não pode ser distinguida de um círculo, ela é incluída na ordem circular, ou sacerdotal, e essa é classe mais alta de todas. (Abbott 2002:12 [25-6])
Em nosso mundo há uma lei da natureza que determina que uma criança do sexo masculino terá um lado a mais do que seu pai, de modo que cada geração se eleva (por via de regra) um degrau na escala de desenvolvimento e nobreza. […] Mas essa regra não se aplica sempre aos comerciantes, e ainda menos freqüentemente aos soldados e aos trabalhadores, que na verdade mal merecem ser chamados de figuras humanas, já que não têm todos os lados iguais. (Abbott 2002:12 [26])
Raramente – em comparação ao imenso número de nascimentos de isósceles – pais isósceles geram um genuíno triângulo de lados iguais que possa receber o certificado de eqüilátero. […] O nascimento de um verdadeiro triângulo eqüilátero de pais isósceles é motivo de júbilo em nosso país. Depois de um exame minucioso feito pelo Conselho Sanitário e Social, a criança, caso receba o certificado de regular, é admitida em cerimônia solene à classe de eqüiláteros. É então imediatamente tirada de seus orgulhosos embora tristes pais e adotada por algum eqüilátero sem filhos, que jura perante a lei nunca mais permitir que a criança entre em seu lar anterior ou que sequer aviste seus parentes novamente, para evitar que o organismo recém desenvolvido possa, por força de imitação inconsciente, retroceder para seu nível hereditário. (Abbott 2002:12-3 [26-7])
O surgimento ocasional de um eqüilátero das fileiras de seus ancestrais nascidos servos é bem recebido não apenas pelos próprios servos pobres, como um raio de luz e esperança sobre a monótona esqualidez de suas existências, como também pelos aristocratas em geral, já que todas as classes mais altas sabem muito bem que esse raro fenômeno, ao mesmo tempo em que faz pouco ou nada para popularizar seus próprios privilégios, serve como barreira extremamente útil contra revoltas das classes mais baixas. […] Se a turba de ângulos agudos fosse totalmente, sem exceção, desprovida de esperança e ambição, eles poderiam ter encontrado líderes em algumas de suas muitas insurreições rebeldes que fossem capazes de tornar sua força e maior número demasiados até para a sapiência dos círculos. Mas um sábio ditame da natureza estabeleceu que quando a inteligência, o conhecimento e todas as virtudes aumentam nas classes trabalhadoras, na mesma proporção aumentará também seu ângulo agudo (que os torna fisicamente terríveis), aproximando-se do ângulo comparativamente inofensivo do triângulo eqüilátero. Dessa forma, na mais brutal e perigosa classe dos soldados – criaturas quase do mesmo nível das mulheres, no que diz respeito à sua falta de inteligência – verifica-se que, quando a capacidade mental necessária para tirar vantagem de seu poder de penetração aumenta, diminui o poder de penetração em si. […] Como é admirável essa lei de compensação! Assim como a prova cabal da natural adequação e, eu poderia até dizer, da origem divina da constituição aristocrática dos Estados em Planolândia! Por meio do uso sensato dessa lei da natureza, os polígonos e círculos conseguem quase sempre refrear rebeliões no nascedouro, tirando vantagem da irreprimível e ilimitada confiança da mente humana. As artes também vêm em auxílio da lei e da ordem. Em geral é possível – por meio de uma pequena compressão ou expansão artificial exercida pelos médicos do estado – tornar perfeitamente regulares alguns dos líderes mais inteligentes de uma rebelião, e admiti-los imediatamente nas classes privilegiadas. (Abbott 2002:13-4 [27-8])
Há não menos do que 120 rebeliões registradas em nossos anais, além de 235 revoltas menores, e todas terminaram da mesma forma. (Abbott 2002:14 [28])
4. Sobre as mulheres
Se nossos triângulos muito pontudos da classe dos soldados são perigosos, pode-se inferir facilmente que muito mais perigosas são nossas mulheres. Pois, se um soldado é uma cunha, uma mulher é uma agulha, sendo, por assim dizer, só pontas, ao menos nas duas extremidades. Acrescente-se a isso o poder de ficar praticamente invisível a qualquer hora, e pode-se ver que uma fêmea, em Planolândia, é uma criatura que não se deve de forma alguma menosprezar. (Abbott 2002:15 [29])
[Leis: ]1. Toda casa terá uma entrada no lado leste para uso exclusivo das mulheres, pela qual todas as fêmeas entrarão de um “modo decoroso e respeitoso” e não pela porta dos homens ou porta ocidental. 2. Nenhuma mulher andará por qualquer local público sem repetir continuamente seu brado de paz, sob pena de morte. 3. Qualquer fêmea que comprovadamente sofra de dança de-são-vito, convulsões, resfriado crônico acompanhado de espirros violentos, ou de qualquer moléstia que provoque movimentos involuntários, será instantaneamente exterminada. (Abbott 2002:15-6 [30])
É considerada uma desgraça para qualquer estado que a legislação tenha de fazer valer o que deveria ser, e é em toda fêmea respeitável, um instinto natural. O movimento rítmico e, se posso assim dizer, bem modulado das costas de nossas senhoras da classe circular é invejado e imitado pela esposa de um eqüilátero comum, que não consegue mais do que um monótono vaivém, como o tique-taque de um pêndulo. E o tique-taque regular do eqüilátero não é menos admirado e copiado pela esposa do progressista isóscele que aspira ascender socialmente, fêmeas em cujas famílias nenhum “movimento das costas” de qualquer espécie se tornou ainda uma necessidade da vida. Portanto, em toda família de posição e respeito, o “movimento das costas” é tão predominante quanto o tempo, e os maridos e filhos nesses lares gozam de imunidade, ao menos, a ataques invisíveis. (Abbott 2002:16-7 [31-2])
Obviamente, portanto, não se deve irritar uma mulher quando ela está em uma posição na qual ela pode girar. (Abbott 2002:17 [32])
A meus leitores de Espaçolândia, a condição de nossas mulheres pode parecer verdadeiramente deplorável, e de fato o é. Um macho do tipo mais baixo de isóscele pode ter a expectativa de alguma melhoria em seu ângulo, e, no final, a ascensão de toda a sua aviltada casta, mas nenhuma mulher pode alimentar tais esperanças para seu sexo. “Uma vez mulher, sempre mulher”, é uma lei da natureza, e as próprias leis da evolução parecem suspensas em seu detrimento. No entanto, ao menos podemos admirar o sábio arranjo prévio que estabeleceu que, como não têm esperanças, as mulheres também não terão memória para relembrar, e nenhuma capacidade para prever as angústias e humilhações, que são ao mesmo tempo uma necessidade de sua existência e a base da constituição de Planolândia. (Abbott 2002:18 [34])
5. De nossos métodos para reconhecermos uns aos outros
O primeiro meio de reconhecimento é o sentido da audição, […] que nos permite não apenas distinguir pela voz nossos amigos, como até discriminar as diferentes classes, pelo menos no que diz respeito às três classes sociais mais baixas, os eqüiláteros, os quadrados e os pentágonos – pois deixo de lado os isósceles. Mas, à medida em que subimos na escala social, o processo de discriminar e ser discriminado pela audição fica mais difícil […]. E toda vez que há perigo de impostura não podemos confiar nesse método. (Abbott 2002:19 [35-6])
Tocar é, entre as nossas mulheres e nas classes mais baixas […] o principal critério de reconhecimento – ao menos entre estranhos, e quando o problema é relativo a classe, e não ao indivíduo. […] “Permita-me pedir que você toque e seja tocado por meu amigo, o senhor Fulano de Tal” – ainda é, entre os mais antiquados de nossos senhores rurais nas regiões distantes das cidades, a fórmula para apresentações em Planolândia. […] [N]ão é necessário, como regra geral, tocar em mais de um único ângulo de um indivíduo, e isso revela a classe da pessoa com quem estamos falando, a menos que de fato ela pertença às partes mais altas da nobreza. Lá a dificuldade é muito maior. (Abbott 2002:19 [36-7])
Ouvi dizer que meu eminente avô – um dos menos irregulares de sua infeliz classe de isósceles, que deveras recebeu, pouco antes de seu falecimento, quatro dos sete votos do Conselho Sanitário e Social para ser transferido para a classe dos eqüiláteros – muitas vezes lastimou, com uma lágrima em seu venerável olho, um acidente […] ocorrido com seu tataravô, um respeitável trabalhador com ângulo ou cérebro de 59 graus e 30 minutos. De acordo com seu relato, meu infeliz ancestral – que sofria de reumatismo -, no instante em que estava sendo tocado por um polígono, em um repentino movimento brusco, acidentalmente trespassou o grande homem na diagonal. Desse modo, parcialmente em conseqüência do longo período em que ficou encarcerado e da prolongada degradação, e parcialmente por causa do choque moral que afetou todos os parentes, meu tataravô lançou a família um grau e meio de volta em sua ascensão rumo a coisas melhores. O resultado foi que na geração seguinte o cérebro da família foi registrado como apenas de 58 graus, e só depois do lapso de cinco gerações é que o terreno perdido foi recuperado, os 60 graus atingidos, e a ascensão da classe dos isósceles finalmente conseguida. E toda essa série de calamidades surgiu a partir de um pequeno acidente durante o processo de tocar. (Abbott 2002:20 [37-8])
[E]mbora não possamos ver ângulos, podemos inferi-los, e com muita precisão. Nosso tato, estimulado pela necessidade e desenvolvido durante um longo treinamento, permite-nos distinguir ângulos com precisão muito maior do que sua visão sem a ajuda de régua ou do transferidor. (Abbott 2002:21 [38])
Há em nosso mundo uma lei da natureza segundo a qual o cérebro da classe dos isósceles se inicia com meio grau, ou 30 minutos, e cresce (quando cresce) de meio grau a cada geração até que o objetivo de 60 graus seja alcançado, quando então a condição de servidão cessa e o homem livre ingressa na classe dos regulares. (Abbott 2002:21 [38])
6. Do reconhecimento pela visão
É apenas entre as classes mais altas e em nossos climas temperados que o reconhecimento pela visão é praticado. […] Essa capacidade existe em qualquer região e para qualquer classe devido à neblina que prevalece durante a maior parte do ano em toda parte, exceto nas zonas tórridas. Ela, que entre vocês de Espaçolândia é claramente um mal, eclipsando a paisagem, deprimindo os espíritos e debilitando a saúde, por nós é reconhecida como uma bênção, certamente em nada inferior ao próprio ar, e parteira das artes e mãe das ciências. (Abbott 2002:22 [40])
Se a neblina não existisse [e nem a miopia], todas as linhas pareceriam iguais e indistintamente claras. E isso é de fato o que acontece naqueles infelizes países nos quais a atmosfera é perfeitamente seca e transparente. Mas, sempre que há um rico suprimento de neblina, os objetos que estão à distância[, digamos, de 90 centímetros, são apreciavelmente mais indistintos do que aqueles que estão a uma distância de 89 centímetros]. E o resultado é que por meio de cuidadosas e constantes observações experimentais da comparativa indistinção e clareza, conseguimos inferir com grande exatidão a configuração do objeto observado. (Abbott 2002:22 [40-1])
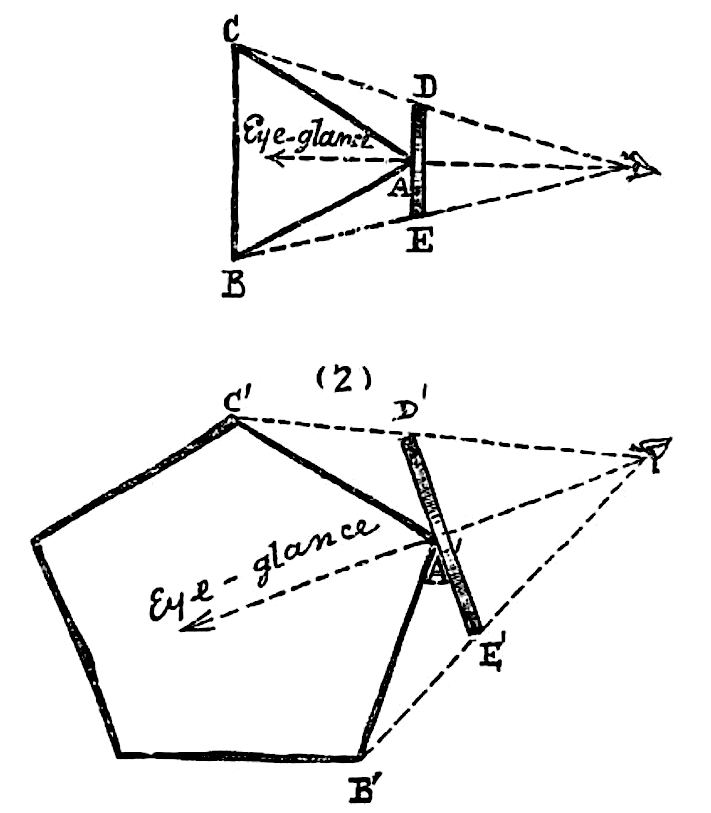
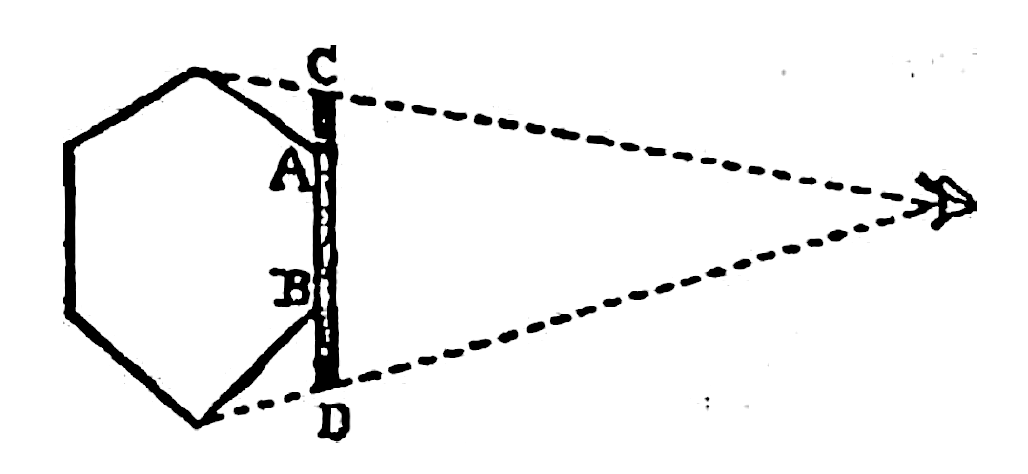
O matemático mais medíocre de Espaçolândia vai prontamente crer em mim quando eu afirmar que os problemas da vida que se apresentam para os cultos – quando estão em movimento, girando, avançando ou retrocedendo, e ao mesmo tempo tentando discriminar por meio da visão entre vários polígonos de alta posição social que se movem em direções diferentes, como, por exemplo, em um salão de baile ou em uma reunião social – devem exigir demais da angularidade dos mais intelectuais e justificam amplamente as gordas doações dos Doutos Professores de Geometria, tanto Estática quanto Cinética, à ilustre Universidade de Wentbridge, onde a Ciência e a Arte do Reconhecimento Visual são ministradas regularmente a grandes turmas formadas pela elite dos estados. (Abbott 2002:24 [43])
Mesmo para mim, um matemático de posição nada medíocre, e avô de dois hexágonos auspiciosos e perfeitamente regulares, descobrir-me em meio a um grupo de polígonos de classe alta girando é às vezes muito desconcertante. […] Resumindo, para se comportar com perfeito decoro na sociedade poligonal é necessário ser um polígono. Pelo menos esse é o doloroso ensinamento de minha experiência. (Abbott 2002:24 [43-4])
Quem no início da vida recorre a “tocar” nunca vai aprender a “ver” com perfeição. […] Por essa razão, entre nossas classes superiores, o ato de “tocar” é desencorajado ou totalmente proibido. Desde o berço, as crianças, ao invés de irem para as escolas públicas de primeiro grau (onde a arte do “tocar” é ensinada), são mandadas a estabelecimentos de ensino superior de caráter exclusivo. E na nossa ilustre universidade, “tocar” é encarado como falha muito séria, implicando suspensão na primeira vez e expulsão na segunda. […] Mas entre as classes mais baixas, a arte do reconhecimento visual é encarada como um luxo inatingível. (Abbott 2002:25 [44])
7. Sobre figuras irregulares
Se nossos lados fossem desiguais, nossos ângulos seriam desiguais. Ao invés de ser suficiente tocar ou estimar visualmente um único ângulo para determinar a forma de um indivíduo, seria necessário determinar cada ângulo por meio do experimento de tocar. Mas a vida seria curta demais para todo esse maçante apalpar. A ciência e a arte do reconhecimento visual iriam imediatamente desaparecer. Tocar, na medida em que é uma arte, não permaneceria por muito tempo, as relações ficariam perigosas ou impossíveis, seria o fim de toda a sensação de confiança, de toda capacidade de prever, ninguém se sentiria seguro para planejar nenhum evento social, por mais simples que fosse. Resumindo, a civilização recairia na barbárie. (Abbott 2002:26 [46-7])
Se fosse permitida a existência de um homem com uma frente triangular e costas poligonais, e que ele propagasse uma descendência ainda mais irregular, o que seria das artes da vida? Devem todas as casas, portas e igrejas de Planolândia ser alteradas para acomodar tais monstros? Devem nossos bilheteiros medir o perímetro de cada homem antes de permitir que entre no teatro, ou se acomode em uma sala de conferência? Os irregulares devem ser dispensados da milícia? E se não, como se pode impedir que eles levem a devastação às fileiras de seus camaradas? Além disso, que tentações irresistíveis de cometer embustes fraudulentos devem forçosamente atacar tal criatura! Como seria fácil para ele entrar em uma loja com sua frente poligonal e encomendar mercadorias a um comerciante crédulo! Por mais que os defensores de uma falsa filantropia pleiteiem a revogação das leis penais para os irregulares, eu nunca conheci um irregular que não fosse também o que a natureza evidentemente tinha a intenção de que fosse – um hipócrita, misantropo e, nos limites de suas capacidades, um praticante de todo tipo de maldade. (Abbott 2002:27-8 [48-9])
8. Da antiga prática da pintura
Dizem que um indivíduo – um pentágono cujo nome não se sabe ao certo -, tendo descoberto casualmente os componentes das cores mais simples e um método rudimentar de pintura, começou a ornamentar primeiro sua casa e depois seus escravos, seu pai, seus filhos, netos e finalmente a si mesmo. […] A moda pegou como fogo no mato. […] A grandiosidade e a glória do desenvolvimento sensorial daquela época são indicadas em parte pela linguagem e pelo vocabulário do período. (Abbott 2002:28-30 [50-2])
9. Da lei universal da cor
Mas, enquanto isso, as artes intelectuais estavam se deteriorando rapidamente. (Abbott 2002:30 [53])
Ano a ano os soldados e os artesãos começaram a afirmar mais veementemente – e com cada vez mais razão – que não havia muita diferença entre eles e as classes mais altas de polígonos, agora que eles haviam sido elevados à igualdade com estes últimos, e capacitados a lidar com todas as dificuldades e a resolver todos os problemas da vida, fossem eles estáticos ou cinéticos, pelo simples processo de reconhecimento pela cor. […] Logo começaram a insistir que, na medida em que a cor, que era uma segunda natureza, havia acabado com a necessidade de distinções aristocráticas, a lei deveria seguir o mesmo caminho, e que dali em diante todos os indivíduos e todas as classes deveriam ser reconhecidas como absolutamente iguais e merecedoras dos mesmos direitos. Eles, portanto, apresentaram a uma assembléia geral extraordinária de todos os Estados de Planolândia um projeto de lei propondo que em cada mulher a metade que contém o olho e a boca deveria ser pintada de vermelho e a outra metade, de verde. Os sacerdotes deveriam também ser pintados, usando-se o vermelho no semicírculo em que o olho e a boca formavam o ponto médio, enquanto o outro semicírculo, o de trás, deveria ser colorido de verde. (Abbott 2002:30-1 [53-4])
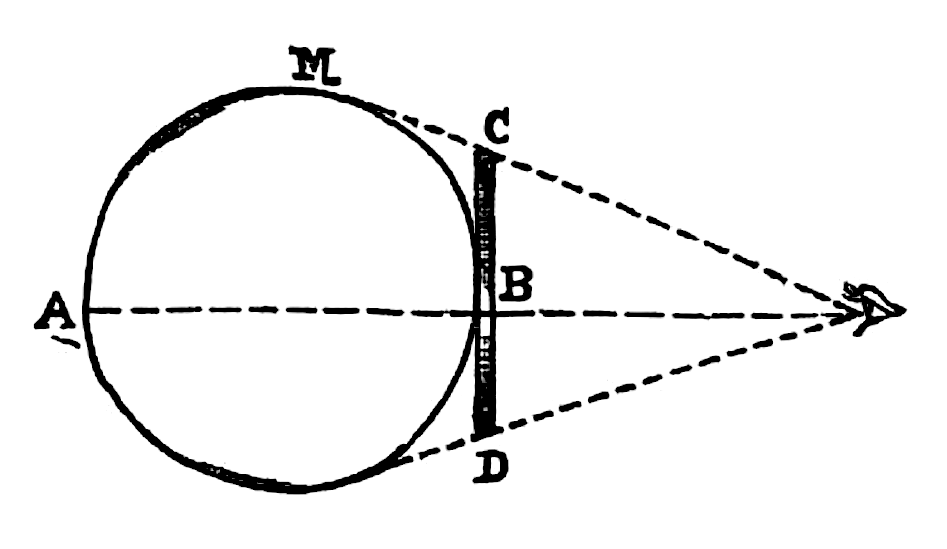
Tenha em mente o declínio do reconhecimento pela visão que ameaçava a sociedade na época da Revolta das Cores; acrescente a certeza de que as mulheres rapidamente aprenderiam a atenuar suas extremidades para imitar os círculos, e então vai ficar certamente óbvio para você, meu caro leitor, que a Lei da Cor nos colocou em grande perigo de confundir um sacerdote com uma jovem. […] O quanto essa possibilidade deve ter sido sedutora para o sexo frágil pode prontamente ser imaginado. […] Assim, aos poucos, o brilho intelectual da classe sacerdotal declinaria e o caminho estaria então aberto para a total destruição de todo o legislativo aristocrático e para a subversão de nossas classes privilegiadas. (Abbott 2002:32-3 [55-7])
10. Da supressão da Rebelião Cromática
Parecia que os sacerdotes não tinham alternativa além de submissão ou extermínio, quando de repente o curso dos acontecimentos foi mudado completamente por um desses pitorescos incidentes que os estadistas não deveriam jamais desprezar, sempre antever, e, às vezes, talvez criar, devido ao poder absurdamente desproporcional com o qual eles apelam para a simpatia do populacho.(Abbott 2002:33 [58])
Aconteceu de um isóscele de um tipo inferior, com um cérebro de pouco mais de quatro graus, se tanto – ao acidentalmente chapinhar nas cores de um comerciante cuja loja ele havia roubado -, pintar a si mesmo, ou fazer-se pintar (a história varia) com as doze cores de um dodecágono. A caminho do mercado ele abordou uma jovem disfarçando a voz – a filha órfã de um nobre polígono, cuja afeição ele havia em vão tentado conquistar no passado. Por meio de uma série de imposturas – ajudado, por um lado, por uma cadeia de golpes de sorte longa demais para ser relatada, e, por outro, por uma insensatez quase inconcebível e um desleixo para com as precauções normais por parte dos parentes da noiva – ele conseguiu consumar o casamento. A infeliz moça cometeu o suicídio ao descobrir o embuste ao qual ela havia sido submetida. Quando a notícia da catástrofe se espalhou pelos Estados, as mentes femininas ficaram violentamente agitadas. Simpatia pela pobre vítima e expectativas de logros semelhantes para si mesmas, suas irmãs e filhas, fizeram com que elas vissem a Lei da Cor de um ponto de vista totalmente novo. Não poucas abertamente se confessaram convertidas à oposição. O resto só precisava de um pequeno estímulo para fazer o mesmo. Agarrando essa oportunidade favorável, os círculos rapidamente convocaram uma assembléia extraordinária dos Estados e, além da usual guarda de condenados, garantiram a presença de um grande número de reacionárias. (Abbott 2002:34 [58-9])
Os círculos não hesitaram em levar sua vitória até o final. Pouparam os trabalhadores, mas os dizimaram. A milícia de eqüiláteros foi imediatamente convocada, e cada triângulo suspeito de irregularidade com base em provas razoáveis foi exterminado por uma Corte Marcial, sem a formalidade de ser medido com precisão pelo Conselho Social. Os lares dos membros das classes dos militares e dos artesãos foram inspecionados por mais de um ano; cada cidade, vilarejo e aldeia foi sistematicamente expurgado daquele excesso de classes inferiores que havia sido causado pelo não-pagamento do tributo de criminosos às escolas e à universidade, e pela violação das outras leis naturais da Constituição de Planolândia. Assim o equilíbrio das classes foi novamente restaurado. […] Nem é necessário dizer que daí por diante o uso de cores foi abolido, e sua posse, proibida. (Abbott 2002:35 [61])
Portanto, é com grande terror que mesmo hoje nossa aristocracia se lembra da época distante da comoção pela Lei Universal da Cor. (Abbott 2002:36 [62])
11. Sobre nossos sacerdotes
Está mais do que na hora de eu passar dessas breves digressões sobre as coisas de Planolândia para ao evento central deste livro, minha iniciação aos mistérios do espaço. Esse é meu assunto, e tudo o que se passou antes é apenas o prefácio. […] No entanto, antes de dar início a meu verdadeiro assunto, meus leitores sem dúvida esperam algumas observações finais sobre os pilares e esteios da Constituição de Planolândia, aqueles que controlam nossa conduta e moldam nosso destino, os objetos de reverência universal e quase de adoração. Preciso dizer que falo de nossos círculos, ou sacerdotes? (Abbott 2002:36 [63-4])
Entre nós, os sacerdotes administram todos os ofícios, artes e ciências; dirigem as transações comerciais, o exército, a arquitetura, a engenharia, a educação, os negócios públicos, o legislativo, a moralidade, a teologia. Embora não façam nada, são as causas de tudo o que vale a pena ser feito, e que é feito por outros. (Abbott 2002:36 [64])
Embora popularmente todos os que são chamados de círculo sejam considerados como tais, entre as classes mais bem-educadas sabe-se que nenhum círculo é realmente um círculo, mas apenas um polígono com um número muito grande de lados muito pequenos. À medida que o número de lados aumenta, um polígono se aproxima de um círculo, e, quando o número é de fato muito grande, digamos, por exemplo, 300 ou 400, é extremamente difícil que o toque mais delicado sinta qualquer ângulo do polígono. (Abbott 2002:37 [64])
A lei da natureza prescreve duas cláusulas antagônicas que afetam a reprodução dos círculos. Primeiro, que à medida que a raça sobe na escala de desenvolvimento, ele se dá a um passo acelerado. Segundo, que na mesma proporção, a raça fica menos fértil. Conseqüentemente, no lar de um polígono de 400 ou 500 lados, é raro encontrar um filho, e impossível haver mais de um. Por outro lado, sabe-se do filho de um polígono de 500 lados que tinha 550, ou até mesmo 600 lados. (Abbott 2002:37 [64-5])
A arte também intervém para auxiliar o processo de evolução superior. Nossos médicos descobriram que os lados pequenos e tenros de um polígono criança da classe mais alta podem ser fraturados e toda a sua compleição recomposta com tanta exatidão que um polígono de 200 ou 300 lados às vezes – não sempre, porque o processo é acompanhado de grave risco -, e somente às vezes, salta 200 ou 300 gerações e, por assim dizer, dobra de um só golpe o número de lados em relação ao de seus progenitores, assim como a nobreza de seus descendentes. (Abbott 2002:37 [65])
12. Da doutrina de nossos sacerdotes
A doutrina dos círculos pode ser rapidamente resumida em uma única máxima: “Cuide de sua configuração“. […] É mérito dos círculos que eles tenham efetivamente suprimido aquelas antigas heresias que levavam os homens a desperdiçar energia e compaixão na crença vã de que a conduta depende de vontade, esforço, treino, encorajamento, elogio ou de qualquer outra coisa que não a configuração. (Abbott 2002:38 [66])
Constantemente executando a política que faz da configuração a idéia diretriz de todas as mentes, os círculos inverteram a natureza do preceito que, na Espaçolândia, regula as relações entre pais e filhos. Entre vocês, as crianças são ensinadas a honrar seus pais. Entre nós – logo depois dos círculos, que são o objeto principal de reverência universal – um homem é ensinado a honrar seu neto, se tiver um. Se não tiver, seu filho. “Honrar”, no entanto, não quer dizer absolutamente “ser indulgente”, mas ter uma consideração reverente por seus interesses mais elevados, e os círculos ensinam que o dever dos pais é subordinar seus próprios interesses àqueles da descendência, promovendo assim o bem-estar do Estado como um todo, assim como o de seus descendentes imediatos. (Abbott 2002:39 [68])
O ponto fraco do sistema dos círculos – se um humilde quadrado se permite falar de qualquer coisa circular como passível de conter algum elemento de fraqueza – parece estar em suas relações com as mulheres. […] O cuidado na escolha de uma esposa regular parece diminuir à medida que se sobe na escala social. (Abbott 2002:39-40 [68-9)
[A] irregularidade de um macho é uma questão de mensuração, mas, como todas as mulheres são retas, e, portanto, visivelmente regulares, é necessário planejar algum outro meio de verificar o que eu poderia chamar de sua irregularidade invisível, ou seja, as potenciais irregularidades no que tange à possível descendência. Isso é feito por meio de pedigrees cuidadosamente mantidos, que são preservados e supervisionados pelo Estado. Sem um pedigree oficial, nenhuma mulher obtém permissão para se casar. (Abbott 2002:39 [68])
Cerca de 300 anos atrás, foi decretado pelo Círculo Cardeal que, devido à deficiência de razão e à fartura de emoção das mulheres, elas não deveriam mais ser tratadas como racionais, nem receber uma educação intelectual. […] Pois a conseqüência é que, do modo como as coisas estão hoje, nós, homens, temos de levar uma espécie de existência bilíngüe, e eu quase diria bimental. Com as mulheres, falamos de “amor”, “dever”, “certo”, “errado”, “compaixão”, “esperança” e outros conceitos irracionais e emocionais, que não têm existência, e cuja invenção só tem por objetivo controlar as extravagâncias femininas. Mas entre nós, e em nossos livros, temos um vocabulário – e eu diria quase idioma – totalmente diferente. Assim, “amor” torna-se “expectativa de favores”; “dever” torna-se “necessidade” ou “adequação”, e outras palavras são igualmente transmutadas. […] Bem, meu medo é de que esse treinamento duplo, na linguagem e no pensamento, seja um fardo grande demais para os jovens, especialmente quando, na idade de três anos, são afastados dos cuidados maternais e ensinados a desaprender a velha linguagem – exceto para repeti-la na presença de suas mães e enfermeiras – e aprender o vocabulário e o idioma da ciência. (Abbott 2002:40-1 [69-70])
PARTE II – Outros mundos
Admirável mundo novo que tem tais habitantes! (Abbott 2002:42 [71])
13. Como eu tive uma visão de Linhalândia
Era o penúltimo dia do ano de 1999 da nossa era, e o primeiro do Longo Feriado. Depois de me entreter até tarde com minha diversão favorita, a Geometria, havia me recolhido para descansar com um problema não resolvido em mente. À noite, tive um sonho. […] Vi na minha frente uma multidão imensa de pequenas linhas retas (que naturalmente supus serem mulheres) intercaladas com outros seres ainda menores que eram como pontos brilhantes – todos se movendo para lá e para cá na mesma linha reta, e, pelo que pude julgar, com a mesma velocidade. […] Enquanto eles se moviam, um barulho confuso de chilreios ou gorjeios múltiplos vinha de tempos em tempos, mas às vezes eles paravam de se mover, e então havia silêncio. […] Aproximando-me de uma das maiores retas – que eu pensava serem mulheres -, dirigi-me a ela, mas não recebi resposta. Uma segunda e uma terceira tentativas de minha parte foram igualmente ineficazes. Perdendo a paciência com o que me parecia ser uma intolerável grosseria, posicionei minha boca diante da sua para interceptar seu movimento, e ruidosamente repeti minha pergunta: […] – Mulher, o que significa esta aglomeração, e este chilrar estranho e confuso, e este movimento monótono para lá e para cá em uma única linha reta? […] – Não sou mulher coisa nenhuma – respondeu a pequena linha. – Sou o monarca do mundo. Mas vós, de onde vindes invadir meu reino de Linhalândia? – Ao receber essa abrupta resposta, pedi perdão por ter de alguma forma assustado ou melindrado sua Alteza Real. E, identificando-me como um forasteiro, roguei ao rei que me falasse de seus domínios. Mas tive a maior dificuldade para obter qualquer informação sobre questões que realmente me interessavam, porque o monarca não conseguia parar de pressupor que o que lhe era familiar também deveria ser do meu conhecimento, e que eu estava simulando ignorância de pilhéria. (Abbott 2002:42 [73-4])
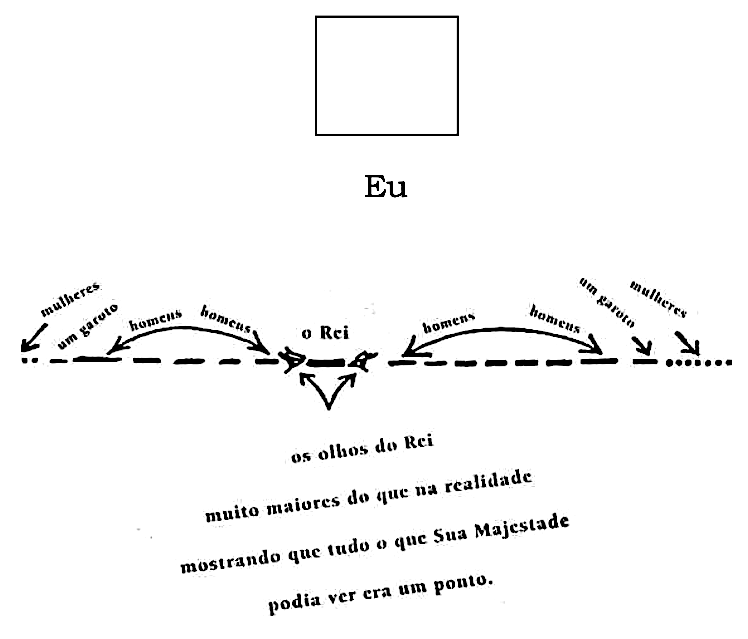
Parecia que este pobre e ignorante monarca – como ele chamava a si mesmo – estava convencido de que a linha reta a que ele chamava de seu reino, e onde vivia, compunha a totalidade do mundo, e, na verdade, a totalidade do espaço. Não sendo capaz de se mover nem de ver, a não ser sua linha reta, ele não tinha qualquer concepção de nada fora dela. […] Fora de seu mundo, ou linha, […] nada existia. (Abbott 2002:43 [74-5])
O movimento e a visão de todos os seus súditos – dentre os quais as pequenas linhas eram homens e os pontos, mulheres – eram limitados àquela única linha reta, que era o mundo deles. Nem é preciso acrescentar que a totalidade do horizonte deles limitava-se a um ponto, e ninguém podia jamais ver coisa alguma que não fosse isso. […] Só pelo som da voz podiam o sexo ou a idade ser distinguidos. […] Ser vizinho para eles era como ser casado para nós. Vizinhos continuavam vizinhos até que a morte os separasse. (Abbott 2002:43-4 [75])
[O monarca disse: ]A proximidade é desnecessária para a união de corações, e o nascimento de filhos é uma questão importante demais para depender de um acidente como a proximidade. Não é possível que o senhor ignore isso. No entanto, já que lhe apraz fingir ignorância, vou instruí-lo como se o senhor fosse o mais pequenino dos nenês de Linhalândia. Saiba, então, que os casamentos são consumados por meio da capacidade de emitir sons e do sentido da audição. O senhor, é claro, sabe que todo homem tem duas bocas, ou vozes (assim como dois olhos) uma voz de baixo e uma voz de tenor, cada qual em uma extremidade. Eu não deveria mencionar isto, mas não consegui perceber sua voz de tenor durante nossa conversa. […] Eu retruquei que só possuía uma voz, e que não tinha percebido que Sua Alteza Real tinha duas. […] – Isso confirma minha impressão – disse o rei – de que o senhor não é um homem, mas, sim, uma monstruosidade feminina com voz de baixo e um ouvido totalmente inculto. Mas, continuando… Tendo a própria natureza disposto que todo homem deve se casar com duas esposas… […] – Por que duas? – perguntei. […] – O senhor leva sua simulação de simplicidade longe demais – exclamou ele. (Abbott 2002:44 [76])
[O monarca disse: ]- Uma vez no meio de cada semana uma lei da natureza nos compele a nos movermos para lá e para cá com um movimento rítmico mais violento do que o usual, e que dura o tempo que o senhor levaria para contar até 101. No meio dessa dança coral, na pulsação de número 51, os habitantes do universo param repentinamente e cada indivíduo emite seu acorde mais suave, doce. É nesse momento decisivo que todos os casamentos são celebrados. As adaptações do baixo à soprano e do tenor à contralto são tão refinadas que freqüentemente os amantes, embora a mil léguas de distância, reconhecem de imediato o som que seu prometido emite em resposta, e, vencendo o insignificante obstáculo da distância, o amor une os três. O casamento que é consumado naquele instante resulta em prole tríplice de macho e fêmeas, a qual assume o seu lugar em Linhalândia. […] – O quê? Sempre tríplice? – disse eu. – Uma esposa então sempre tem trigêmeos? […] – É, ó monstruosidade com voz de baixo! – retrucou o rei. – De que outro modo o equilíbrio entre os sexos seria mantido se não nascessem duas garotas para cada menino? Então você ignora o próprio Alfabeto da Natureza? […] Ele parou de falar, tanta era a raiva, e algum tempo se passou antes que eu conseguisse induzi-lo a retomar sua narrativa. (Abbott 2002:45 [76-7])
[O monarca disse: ]- Não pense, é claro, que todo solteiro entre nós encontra suas parceiras na primeira tentativa desse coro universal de casamento. Pelo contrário, o processo é repetido muitas vezes pela maioria de nós. […] E depois de muitos ensaios e muitos ajustes, o resultado é finalmente alcançado. Finalmente chega um dia em que, enquanto o habitual coro matrimonial se eleva da Linhalândia universal, os três amantes distantes repentinamente se descobrem em perfeita harmonia e, antes de tomarem consciência, a trinca casada é arrebatada vocalmente e levada a um abraço duplo, e a natureza se regozija com mais um casamento e três nascimentos. (Abbott 2002:45 [77-8])
14. Como em vão tentei explicar a natureza de Planolândia
[O monarca disse: ]- Minhas esposas, que neste momento estão ouvindo o som de uma de minhas vozes imediatamente seguida do som da outra, e percebendo que a segunda as alcança depois de um intervalo no qual o som pode percorrer 16,4 centímetros, inferem que uma de minhas bocas está 16,4 centímetros mais distante delas do que a outra, e, dessa maneira, sabem que meu formato é de 16,4 centímetros Mas você obviamente entende que minhas esposas não fazem esse cálculo todas as vezes que ouvem minhas duas vozes. Elas o fizeram de uma vez por todas antes de nos casarmos. Mas elas poderiam fazê-lo a qualquer hora. E, da mesma forma, eu posso estimar o formato de qualquer um dos meus súditos do sexo masculino por meio do sentido da audição. (Abbott 2002:46 [80])
[Repliquei: ]- Além dos seus movimentos para o norte e para o sul, existe outro movimento, que eu chamo de da direita para a esquerda.
– Mostre-me, por favor, esse movimento da esquerda para a direita.
– Não, não posso, a menos que Vossa Alteza pudesse sair totalmente da sua linha.
– Sair da minha linha? Você quer dizer do mundo? Do espaço?
– Bem, é. Sair do seu mundo. Para fora do seu espaço. Pois o seu espaço não é o verdadeiro espaço. O verdadeiro espaço é um plano, e o seu espaço não passa de uma linha.
– Se o senhor não consegue mostrar este movimento da esquerda para a direita fazendo o movimento, então eu rogo que o descreva para mim em palavras.
– Se Vossa Alteza não consegue distinguir seu lado direito do esquerdo, temo que não existam palavras que possam transmitir o que eu quero dizer. Mas com certeza Vossa Alteza não pode ignorar uma distinção tão simples.
– Não o entendo nem um pouco.
– Ai de mim! Como é que eu vou esclarecer isso? (Abbott 2002:48 [81-2])
– Bem, já que as palavras não conseguem explicar, vou tentar os atos, e vou me mover gradualmente para fora de Linhalândia na direção que eu desejo indicar a Vossa Alteza. Ao dizer isso, comecei a tirar meu corpo de Linhalândia. […] Enquanto uma parte de mim continuava em seus domínios e à sua vista, o rei ficou exclamando:
– Estou vendo você, ainda estou vendo. Você não está se movendo. Mas quando finalmente eu me retirei totalmente de sua linha, ele exclamou em sua voz mais estridente:
– Ela desapareceu. Ela morreu!
– Não morri – repliquei. (Abbott 2002:48 [82-3]])

O senhor me pede que acredite que existe outra linha além daquela que meus sentidos indicam, e outro movimento além daquele do qual eu estou diariamente consciente. Eu, em troca, peço ao senhor que descreva em palavras ou indique por meio de movimento a outra linha da qual fala. Em vez de se mover, o senhor meramente faz um truque de magia; desaparece e volta a ficar visível. E em vez de qualquer descrição lúcida de seu mundo novo, simplesmente me diz quantos são e os tamanhos de uns quarenta de meu séquito, coisas que qualquer criança da minha capital sabe. Tem alguma coisa mais irracional ou insolente do que isso? (Abbott 2002:49 [83-4])
15. Sobre um forasteiro de Espaçolândia
Era o último dia do ano de 1999 de nossa era. […] Eu estava absorto em pensamentos, refletindo sobre algumas palavras que haviam casualmente saído da boca de meu neto mais jovem, um hexágono muito promissor, de brilhantismo incomum e angularidade perfeita. […] Pegando nove quadrados, cada um com lado de um centímetro, eu os havia colocado juntos para formar um quadrado grande com três centímetros de lado, e então tinha provado para meu netinho que – embora fosse impossível para nós vermos dentro do quadrado – poderíamos determinar seu número de centímetros quadrados simplesmente elevando ao quadrado o número de centímetros do lado.
– E assim – disse eu – sabemos que 32, ou nove, representa a área de um quadrado cujo lado tem três centímetros de comprimento. […] O pequeno hexágono meditou sobre isso por um tempo e depois me disse:
– Mas você tem me ensinado a elevar números à potência de três. Suponho que 33 deva significar alguma coisa em Geometria. O que significa?
– Nada – disse eu -, pelo menos não na Geometria, porque ela trata apenas de duas dimensões. […] E então passei a mostrar ao garoto como um ponto, movendo-se por uma distância de três centímetros, forma uma linha de três centímetros, que pode ser representada por três, e como uma linha de três centímetros, movendo-se em paralelo a si mesma por três centímetros, forma um quadrado de três centímetros de lado, que pode ser representado por 32. […] Após essas considerações, meu neto, voltando novamente à sua sugestão anterior, subitamente me interpelou, exclamando:
– Bem, então, se um ponto, ao se mover por três centímetros, forma uma linha de três centímetros representada por três, e se uma linha reta de três centímetros, ao se mover em paralelo a si mesma, forma um quadrado de três centímetros de lado, representado por 32, um quadrado de três centímetros de lado, movendo-se em paralelo a si mesmo (embora eu não veja como), deve formar alguma outra coisa (embora eu não veja o quê) de três centímetros de lado: e isso deve ser representado por 33.
– Vá para a cama – disse eu, um tanto irritado com a interrupção. – Se você falasse menos disparates, lembraria de mais coisas sensatas. (Abbott 2002:50-1 [86-7])
[Eu disse: ]- O garoto é um tolo. […] Na Geometria, 33 não pode ter significado. […] Imediatamente surgiu uma resposta claramente audível:
– O garoto não é um tolo, e 33 tem um significado geométrico óbvio. […] Tanto minha esposa quanto eu ouvimos essas palavras, embora ela não soubesse o que queriam dizer, e nós dois nos arremessamos para frente na direção do som. (Abbott 2002:51 [87])
Dei uma olhada na ampulheta. Os últimos grãos de areia tinham caído. O terceiro milênio havia começado. (Abbott 2002:52 [88])
16. Como o forasteiro em vão tentou me revelar em palavras os mistérios de Espaçolândia
[A esfera disse: ]- Ora bolas! O que sabe o senhor do espaço? Defina espaço.
– Espaço, meu senhor, é altura e largura prolongadas indefinidamente.
– Exatamente. Vê-se que nem sabe o que é espaço. O senhor acha que tem apenas duas dimensões, mas eu vim apresentar ao senhor uma terceira: altura, largura e extensão.
– Vossa senhoria se apraz em se divertir. Também falamos de extensão e altura, ou largura e espessura, dessa forma denotando duas dimensões por quatro nomes.
– Mas me refiro não apenas a três nomes, mas a três dimensões.
– Vossa senhoria indicaria ou explicaria para mim em qual direção fica a terceira dimensão que eu ignoro?
– Eu vim dela. Fica para cima e para baixo.
– Vossa senhoria quer dizer aparentemente que fica para o norte e para o sul.
– Não quero dizer nada disso. Refiro-me à direção para a qual o senhor não pode olhar porque não possui olhos neste lado. (Abbott 2002:53-4 [90])
Quando nós, de Planolândia, vemos uma linha, vemos extensão e brilho. Se o brilho desaparece, a linha se extingue, e, como vossa senhoria diz, deixa de ocupar espaço. Será que devo entender que vossa senhoria dá ao brilho o nome de uma dimensão, e que o que chamamos de “brilhante” o senhor chama de “alto”?
– Na verdade, não. Por “altura” eu me refiro a uma dimensão como a sua extensão; só que, para vocês, a “altura” não é tão facilmente perceptível por ser extremamente pequena.
– Meu senhor, sua afirmação pode ser facilmente testada. Vossa senhoria diz que eu tenho uma terceira dimensão à qual chama de “altura”. Ora, dimensão implica direção e medida. Então, meça minha “altura”, ou indique a direção na qual minha “altura” se estende, e eu vou me convencer. Caso contrário, sua atitude há de me justificar.
– Não posso fazer nenhuma das duas coisas. Como vou fazer para convencêlo? (Abbott 2002:55 [92-3])
[A esfera disse: ]Eu não sou uma figura plana, mas, sim, um sólido. […] O senhor não se lembra […] de como, ao entrar no reino de Linhalândia, o senhor foi forçado a se manifestar para o rei não como um quadrado, mas como uma linha, porque aquele reino linear não tinha dimensões suficientes para que sua totalidade fosse representada, e apenas uma fatia ou seção sua podia ser representada? Exatamente da mesma forma, seu país de duas dimensões não é espaçoso o suficiente para que eu, um ser de três dimensões, seja representado, e só pode exibir uma fatia ou seção minha, que é o que o senhor chama de círculo. O brilho reduzido de seus olhos indica incredulidade. (Abbott 2002:55-6 [93])
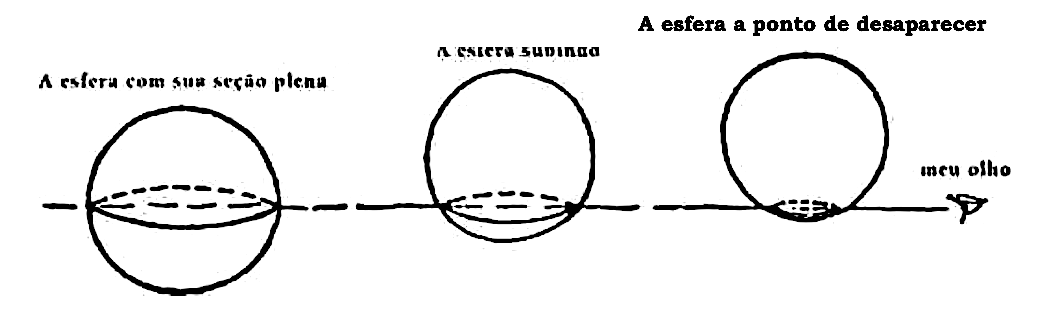
[E]mbora eu visse os fatos na minha frente, as causas continuavam obscuras. Tudo o que eu conseguia entender era que o círculo havia se tornado menor e desaparecera, e que ele tinha agora reaparecido e estava rapidamente se tornando maior. (Abbott 2002:56 [94])
[A esfera perguntou: ]- Diga-me, senhor matemático, se um ponto se move na direção norte e deixa um rastro luminoso, que nome o senhor daria para o rastro?
– Linha reta.
– E uma linha reta tem quantas extremidades?
– Duas.
– Agora, imagine a linha reta que vai para o norte movendo-se em paralelo a si mesma no sentido leste-oeste, de modo que cada ponto dela deixe atrás de si como rastro uma linha reta. Que nome o senhor dará para a figura assim formada? Vamos supor que ela se mova por uma distância igual à linha reta original. Qual seu nome?
– Quadrado.
– E quantos lados tem um quadrado? Quantos ângulos?
– Quatro lados e quatro ângulos.
– Agora, vá um pouco além e imagine um quadrado em Planolândia movendo-se para cima paralelamente a si mesmo.
– Como? Na direção norte?
– Não, não na direção norte. Para cima, saindo totalmente de Planolândia. Se ele se movesse para o norte, os pontos no lado sul do quadrado teriam de se mover passando pelas posições anteriormente ocupadas pelos pontos do lado norte. Mas não é isto que eu estou dizendo. Estou dizendo que cada ponto do senhor (pois o senhor é um quadrado e vai servir como ilustração)[…], quer dizer, daquilo que o senhor chama de seu interior, deve se mover para cima no espaço de tal modo que nenhum ponto passe pela posição anteriormente ocupada por qualquer outro ponto, mas cada ponto vai por si mesmo descrever uma linha reta. (Abbott 2002:57 [95])
[A esfera disse: ]Começamos com um único ponto, que, obviamente (sendo um ponto) só tem um ponto-limite. Um ponto produz uma linha com dois pontos-limites. Uma linha produz um quadrado com quatro pontos-limites. Agora o senhor mesmo pode dar a resposta à sua própria pergunta: um, dois, quatro, estão evidentemente em progressão geométrica. Qual é o próximo número?
– Oito.
– Exatamente. Um quadrado produz uma coisa para a qual o senhor ainda não tem um nome, mas que chamaremos de cubo com oito pontos-limites. Agora está convencido?
– E esta criatura tem lados, além de ângulos, ou o que o senhor chama de “pontos-limites”?
– Claro, e tudo de acordo com a analogia. […]
– E quantos […] lados vão fazer parte deste ser que eu devo gerar pelo movimento de meu interior em uma direção “para cima”, e ao qual o senhor chama de cubo?
– Mas que pergunta! E vinda de um matemático! O lado de qualquer coisa tem sempre, se me é lícito dizê-lo, uma dimensão a menos do que a coisa. Conseqüentemente, como não há dimensão inferior à de um ponto, um ponto tem 0 lados. Uma linha, se permite a expressão, tem dois lados (já que os pontos de uma linha podem ser chamados por deferência especial de seus lados). Um quadrado tem quatro lados. Assim: 0, dois, quatro, qual o nome que o senhor dá a essa progressão?
– Aritmética.
-E qual é o próximo número?
– Seis.
– Exatamente. Portanto, pode ver que o senhor respondeu à sua própria pergunta. O cubo que o senhor vai gerar vai ser limitado por seis lados, ou seja, seis de seus interiores. Agora entendeu tudo, não?
– Monstro – gritei -, seja o senhor prestidigitador, feiticeiro, sonho ou demônio, não vou mais tolerar sua zombaria. Um de nós deve morrer. (Abbott 2002:57-8 [96-7])
17. Como a Esfera, tendo em vão tentado com palavras, recorreu às ações
[A esfera disse: ]Espera, já sei. As ações, e não as palavras, revelarão a verdade. (Abbott 2002:58 [98])
[A esfera disse: ]O que o senhor chama de coisas sólidas são na verdade superficiais. O que o senhor chama de espaço não passa de um grande plano. Eu estou no espaço, e olho de cima para os interiores das coisas das quais o senhor só vê o lado de fora. O senhor mesmo poderia sair deste plano, se o senhor conseguisse ter a vontade necessária para isso. Um leve movimento para cima ou para baixo permitiria que o senhor visse tudo o que eu posso ver. (Abbott 2002:59 [99])
-Ah! É assim? – bradou o forasteiro. – Então, cumpra seu destino: para fora de seu plano. Um, dois, três! Está feito! (Abbott 2002:60 [100])
18. Como fui parar em Espaçolândia, e o que vi por por lá
Fui tomado por um terror indizível. Houve uma escuridão, depois uma vertiginosa e nauseante sensação de ver que não era como ver. Vi uma linha que não era uma linha, um espaço que não era espaço. Eu era eu mesmo e não o era. Quando consegui falar, gritei em agonia:
– Ou isto é a loucura ou é o Inferno.
– Nenhum dos dois – replicou calmamente a voz da esfera -, é o conhecimento, são as três dimensões. Abra os olhos mais uma vez e tente olhar com firmeza. […] Olhei, e eis que lá estava um novo mundo! Lá estava, na minha frente, manifestamente materializado, tudo o que antes eu havia inferido, conjeturado, sonhado, de perfeita beleza circular. […] Olhei para baixo, e vi com meu olho material todas aquelas particularidades domésticas que eu havia até então apenas inferido com o intelecto. E como era pobre e vaga a conjectura inferida em comparação com a realidade que agora eu via! (Abbott 2002:60-1 [101-3)
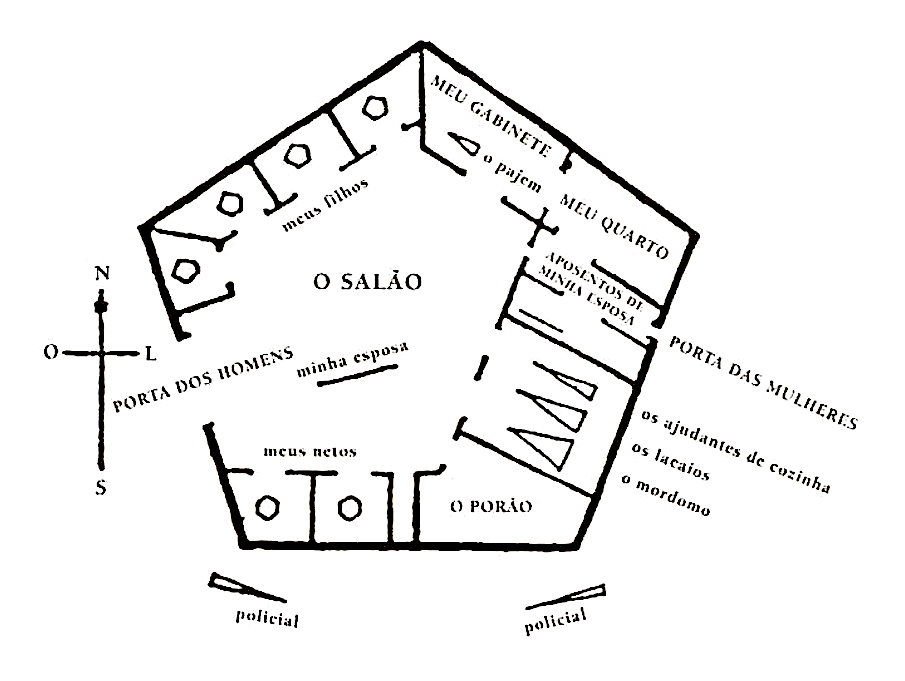
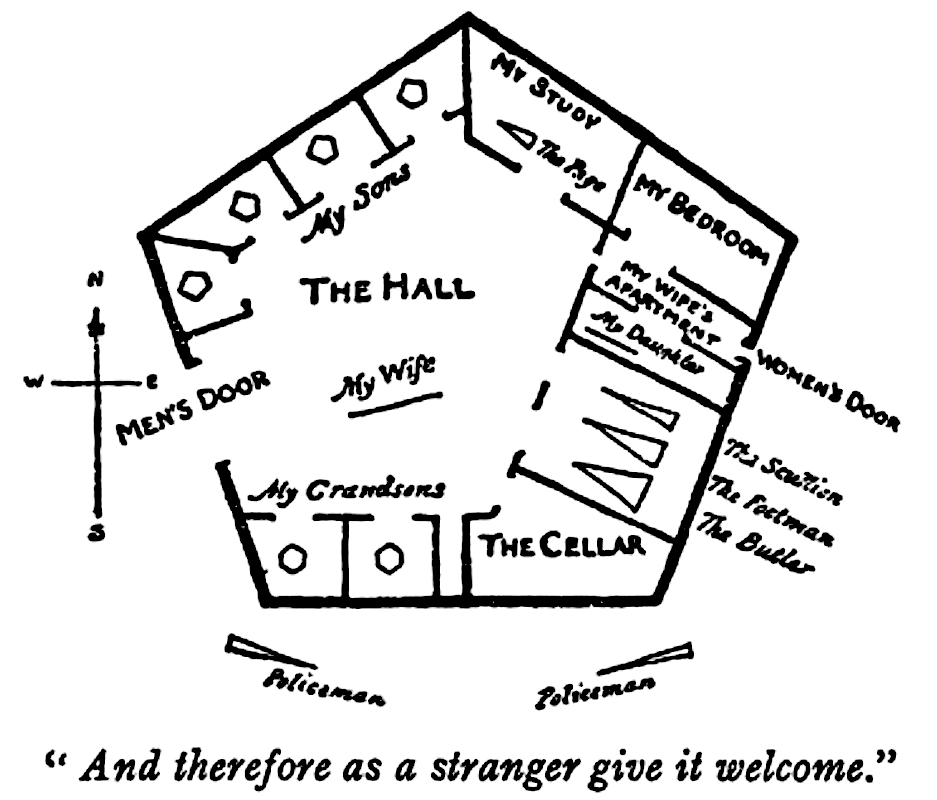
Estupefato com a visão dos mistérios da terra assim desvelados perante meu indigno olho, disse para meu companheiro:
– Veja, tornei-me semelhante a um deus. Pois os sábios de nosso país dizem que ver todas as coisas, ou a onividência, como eles dizem, é atributo apenas de Deus. […] Havia um certo desdém na voz de meu professor quando ele respondeu:
– É mesmo? Então até os batedores de carteira e os assassinos de meu país devem ser adorados por seus sábios como deuses, já que não há um único deles que não veja tanto quanto o senhor está vendo agora. Mas acredite, seus sábios estão enganados. (Abbott 2002:62 [103-4])
– Não compete a mim classificar as faculdades humanas de acordo com seus méritos. No entanto, muitos dos melhores e mais sábios de Espaçolândia têm mais apreço pelos sentimentos do que pela compreensão, pelas suas desprezadas linhas retas do que por seus enaltecidos círculos. (Abbott 2002:62 [104])
19. Como, embora a Esfera me mostrasse outros mistérios de Espaçolândia, eu ainda ansiava por mais, e em que isso resultou
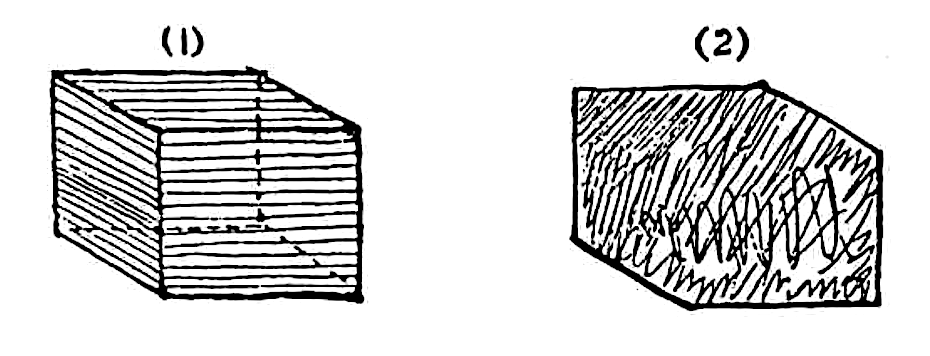
– Perdoe-me, meu senhor – retruquei -, mas para a minha vista a aparência é a de uma figura irregular cujo interior está exposto. Em outras palavras, parece-me que não vejo um sólido, mas um plano como o que inferimos em Planolândia, só que com uma irregularidade própria de um terrível criminoso, cuja mera visão é dolorosa a meus olhos. […] – Exatamente – disse a esfera -, parece-lhe um plano porque o senhor não está acostumado com luz, sombra e perspectiva, da mesma forma como, em Planolândia, um hexágono pareceria ser uma linha reta para quem não conhecesse a arte do reconhecimento pela visão. Mas na realidade é um sólido, como o senhor vai descobrir por meio do tato. (Abbott 2002:65 [108])
Repetir a explicação da esfera para estas questões, por mais sucinta e clara que tenha sido, seria enfadonho para um habitante do espaço, por ser ele conhecedor delas. Basta dizer que, por meio de suas afirmações lúcidas, pela modificação da posição dos objetos e das luzes, e permitindo que eu tocasse em vários objetos e até em sua própria santa pessoa, ele finalmente esclareceu tudo para mim, de tal forma que agora eu podia distinguir entre um círculo e uma esfera, uma figura plana e um sólido. (Abbott 2002:65 [108])
Este foi o clímax, o paraíso de minha estranha e atribulada história. Daqui por diante tenho de relatar a história de minha lamentável queda (Abbott 2002:65 [108-9])
– Senhor, sua própria sabedoria me ensinou a aspirar a alguém ainda maior, mais bonito, e mais próximo da perfeição. Como o senhor, superior a todas as formas de Planolândia, é uma combinação de muitos círculos em um, sem dúvida existe alguém acima, que é uma combinação de muitas esferas em um ente supremo que supera até os sólidos de Espaçolândia. E exatamente como nós, que agora estamos no espaço, olhamos para baixo, para Planolândia, e vemos os interiores de todas as coisas, certamente existe mais acima de nós uma região mais elevada, mais pura, para onde vós sem dúvida tendes o propósito de me levar […][,] um espaço mais espaçoso, uma dimensionalidade mais dimensionável, uma posição vantajosa de onde olharemos juntos para baixo, para os interiores revelados das coisas sólidas, e onde seus intestinos, e os de suas esferas aparentadas, estarão expostos à vista do pobre exilado desgarrado de Planolândia, a quem tanto já foi concedido.
– Ora essa! Tolices! Chega dessas bobagens! O tempo é curto, e ainda há muito a ser feito antes que o senhor esteja pronto para pregar o Evangelho das Três Dimensões a seus compatriotas ignorantes de Planolândia. (Abbott 2002:66 [109-10])
Não fui eu ensinado lá embaixo que quando eu via uma linha e inferia um plano, na realidade eu via uma terceira dimensão não percebida, não a mesma do brilho, chamada de “altura”? E não se segue que, nesta região, quando eu vejo um plano e infiro um sólido, na verdade eu vejo uma quarta dimensão não percebida, não a mesma da cor, mas existente, embora infinitesimal e incapaz de ser medida? E, além disso, há a prova da analogia entre figuras. […] Indubitavelmente não podemos ver aquela outra Espaçolândia mais elevada agora porque não temos olhos em nossos estômagos. Mas, da mesma forma como existia o reino de Planolândia, embora aquele pobre e insignificante monarca de Linhalândia não pudesse virar nem para a direita nem para a esquerda para vê-lo; e da mesma forma como existia, bem à mão, tocando em minha estrutura, a Terra das Três Dimensões, embora eu, cego tolo miserável, não tivesse o poder de tocá-la, nem um olho em meu interior para percebê-la; certamente existe uma quarta dimensão, que meu senhor percebe com o olho interior do pensamento. E isso, o senhor mesmo me ensinou. […] Em uma dimensão, um ponto em movimento não produzia uma linha com dois pontos-limites? Em duas dimensões, uma linha em movimento não produzia um quadrado com quatro pontos-limites? Em três dimensões, um quadrado em movimento não produzia […] aquele bendito ser, o cubo, com oito pontos-limites? E em quatro dimensões, não vai um cubo em movimento (ai da analogia, e ai do progresso da verdade se assim não for) digo, não vai o movimento de um divino cubo resultar em uma organização ainda mais divina com dezesseis pontos-limites? Veja a confirmação infalível da série: dois, quatro, oito, dezesseis. Não é uma progressão geométrica? Isto não está (se me é permitido citar as palavras de meu senhor) “estritamente de acordo com a analogia”? Além disso, não me foi ensinado por meu senhor que, da mesma forma como em uma linha há dois pontos divisórios, e em um quadrado há quatro linhas divisórias, em um cubo deve haver seis quadrados divisórios? Veja mais uma vez a série confirmativa dois, quatro, seis. Não é uma progressão aritmética? E como conseqüência não se segue necessariamente que o produto mais divino do divino cubo na Terra das Quatro Dimensões deva ter oito cubos divisórios, e não está isto, como meu senhor me ensinou a acreditar, “estritamente de acordo com a analogia”? (Abbott 2002:67-8 [111-2])
[S]e de fato é isso, que este outro espaço é realmente Pensamentolândia, então me leve para essa bendita região onde em pensamento verei os interiores de todas as coisas sólidas. Lá, ante meu olho encantado, um cubo, movendo-se em alguma direção totalmente nova, mas estritamente de acordo com a analogia, de tal forma que faça cada partícula de seu interior atravessar um novo tipo de espaço com um rastro todo seu, irá criar uma perfeição ainda mais perfeita que si mesmo, com dezesseis ângulos sólidos extras como limites, e oito cubos sólidos de perímetro. E uma vez lá, será que interromperemos nosso caminho para cima? Naquela bendita região de quatro dimensões, será que hesitaremos no limiar da quinta dimensão e não entraremos lá? Ah, não! Vamos, ao contrário, decidir que nossa ambição vai se elevar junto com nossa subida corporal. E então, rendendo-se a nossa investida intelectual, os portões da sexta dimensão se abrirão, e depois os da sétima e depois os da oitava… (Abbott 2002:66-7 [113])
Para baixo! Eu estava descendo rapidamente, e eu sabia que a volta para Planolândia seria minha perdição. Dei uma olhadela, a última e que nunca seria esquecida, naquela vastidão insípida e plana – que agora viria a se tornar novamente meu universo – estendida à minha frente. Então, a escuridão. Depois, um trovão final, e, quando voltei a mim, eu era mais uma vez um rastejante quadrado comum em meu gabinete, em casa, ouvindo o brado de paz da minha mulher que se aproximava. (Abbott 2002:67 [113-4])
20. Como a Esfera me encorajou em uma visão
Quando finalmente fiquei sozinho, um entorpecimento se abateu sobre mim, mas, antes que meus olhos se fechassem, tentei reproduzir a terceira dimensão, e especialmente o processo por meio do qual um cubo é construído a partir do movimento de um quadrado. Não estava tão claro quanto seria de se desejar, mas lembrei que tinha de ser “para cima, e não para o norte”, e decidi resolutamente reter na memória essa expressão por ser a pista que, se firmemente entendida, me levaria à solução. Então, repetindo mecanicamente, como se fosse uma fórmula mágica, a expressão “para cima, e não para o norte”, caí em um profundo sono reparador. (Abbott 2002:69-70 [115-6])
Durante o sono, tive um sonho. Achei que estava mais uma vez ao lado da esfera, cuja cor brilhante indicava que havia substituído a raiva por uma perfeita tolerância. Estávamos nos movendo juntos em direção a um ponto brilhante, mas infinitesimalmente pequeno, para o qual meu mestre dirigiu minha atenção. […] – Olhai lá – disse meu guia -, em Planolândia vivíeis, de Linhalândia tivestes uma visão, voastes comigo às alturas de Espaçolândia. Agora, a fim de completar vossa experiência, eu vou conduzir-vos para baixo, para o nível mais baixo da existência, para o reino de Pontolândia, o abismo sem dimensões. Olhe lá aquela criatura desprezível. Aquele ponto é um ser como nós, mas confinado ao abismo não dimensional. Seu mundo, seu universo, é ele mesmo. Não pode conceber qualquer outro que não ele mesmo. Não conhece extensão, largura, altura, porque não tem experiência delas. Não tem conhecimento nem do número dois, nem tem idéia da pluralidade. Porque ele é o tudo, já que não é realmente nada. No entanto, observe sua perfeita satisfação consigo mesmo, e daí aprenda esta lição: a de que estar satisfeito consigo mesmo é ser desprezível e ignorante, e que ter aspirações é melhor do que ser cega e impotentemente feliz. (Abbott 2002:70 [116])
“Ele preenche todo o espaço”, continuou a pequena criatura que monologava, “e aquilo que ele preenche, ele é. Aquilo que elo pensa, é o que fala, e o que fala, é o que ouve. E ele mesmo é o que pensa, fala, ouve; o pensamento, a palavra, a audição. E o Um, e o Tudo. Ah, a felicidade, Ah, a felicidade de ser!” (Abbott 2002:70 [117])
[A esfera disse: ]Até onde o monarca compreende o que o senhor disse, ele interpreta como se fosse ele mesmo que o tivesse dito, já que ele não consegue conceber qualquer outro que não ele mesmo, e se vangloria da variedade de “seu pensamento” como um exemplo de poder criativo. Vamos deixar este deus de Pontolândia fruindo ignorantemente sua onipresença e onisciência. Nada do que o senhor ou eu façamos pode resgatá-lo de sua satisfação consigo mesmo. (Abbott 2002:71 [117-8])
Ele ficara aborrecido a princípio – confessou – com minha ambição de voar até dimensões maiores do que a terceira, mas, desde então, ele tinha tido novos insights e não era com orgulho que admitia para um pupilo seu erro. Depois, passou a me iniciar nos mistérios ainda mais elevados do que os que eu havia testemunhado, mostrando-me como construir sólidos extras por meio do movimento dos sólidos, e sólidos extras duplos por meio do movimento dos sólidos extras, e tudo “estritamente de acordo com a analogia”, tudo por meio de métodos tão simples, tão fáceis, que eram evidentes até para o sexo feminino. (Abbott 2002:71 [118])
21. Como tentei ensinar a Teoria das Três Dimensões ao meu neto, e com que resultado
Iria partir imediatamente e evangelizar toda a Planolândia. Até para as mulheres e os soldados, o Evangelho das Três Dimensões deveria ser proclamado. (Abbott 2002:72 [119])
“Para cima, e não para o norte” – era a chave para a prova. Parecia-me muito claro antes de cair no sono, e quando acordei, recém saído do meu sonho, parecera tão evidente quanto a Aritmética, mas, de alguma forma, agora não me parecia tão óbvio. (Abbott 2002:72 [119])
Por que não, portanto, fazer meu primeiro experimento com meu precoce neto, cujas observações casuais sobre o significado de 33 tinham sido aprovadas pela esfera? Discutindo a questão com ele, um mero garoto, eu estaria perfeitamente a salvo, pois ele não saberia da Proclamação do Conselho, ao passo que eu não poderia ter certeza de que meus filhos – já que o patriotismo e a reverência deles pelos círculos predominavam sobre a mera afeição – não fossem se sentir compelidos a me entregar para o governador, se achassem que eu estava defendendo a sério a sediciosa heresia da terceira dimensão. (Abbott 2002:72 [120])
Quando meu neto entrou na sala, cuidadosamente fechei a porta. Depois, sentando a seu lado e pegando tabuinhas matemáticas – ou, como diriam vocês, linhas -, disse a ele que iríamos retomar a aula da véspera. Ensinei a ele novamente como um ponto, ao se mover em uma dimensão, produz uma linha, e como uma linha reta, em duas dimensões, produz um quadrado. Depois disso, forçando uma risada, disse:
– E agora, seu pestinha, você queria que eu acreditasse que um quadrado pode, pelo mesmo movimento “para cima, e não para o norte”, produzir outra figura, uma espécie de quadrado extra em três dimensões. Não é, seu pestinha? […] Neste instante ouvimos mais uma vez o “Ó, sim! Ó, sim!” do arauto na rua, proclamando a Resolução do Conselho. Embora jovem, meu neto – que era extraordinariamente inteligente para sua idade, e havia sido criado para respeitar a autoridade dos círculos – compreendeu a situação com uma sagacidade para a qual eu não estava preparado. Ficou em silêncio até as últimas palavras da Proclamação terem sido ditas, e depois, caindo no choro:
– Querido avô – disse ele – era só brincadeira, e é claro que eu não queria dizer nada com aquilo, e não sabíamos nada sobre a nova lei, e não acho que eu tenha dito nada sobre a terceira dimensão, e tenho certeza de que eu não disse nada sobre “para cima, e não para o norte”, porque isso seria muito absurdo. Como uma coisa pode se mover para cima e não para o norte? Para cima e não para o norte! Mesmo se eu fosse um bebê, eu não falaria uma bobagem dessas. Que tolice! Há! Hã!
– Não é tolice nenhuma – disse eu, perdendo a paciência -, aqui, por exemplo, eu pego este quadrado – e, ao dizer quadrado, peguei um quadrado móvel, que estava à mão – e o movo, está vendo?, Não para o norte, mas… Sim, para cima… Quer dizer, não para o norte, mas para algum lugar… Não exatamente assim, mas… […] Aqui levei minha frase a uma conclusão vã, sacudi o quadrado sem propósito, para o divertimento de meu neto, que caiu na gargalhada mais alto do que nunca, e disse que eu não o estava ensinando, mas, sim, brincando com ele, e, ao dizer isso, destrancou a porta e saiu correndo da sala. Assim terminou minha primeira tentativa de converter um pupilo ao Evangelho das Três Dimensões. (Abbott 2002:72-3 [120-1])
22. Como então tentei difundir a Teoria das Três Dimensões por outros meios, e com que resultado.
Portanto, passei vários meses em segredo na composição de um tratado sobre os mistérios das três dimensões. […] Mas, ao escrever este livro, descobri-me infelizmente tolhido pela impossibilidade de desenhar os diagramas necessários para o meu objetivo, pois, obviamente, em nosso país não há tabuinhas, mas linhas, nem diagramas, mas linhas, todas em uma linha reta e só distinguíveis por meio da diferença de tamanho e brilho, de modo que, quando terminei meu tratado (a que intitulei de “De Planolândia a Pensamentolândia“), não tinha certeza de que seria compreendido. (Abbott 2002:74 [122])
Todos os prazeres se tornaram insípidos, todas as paisagens me atormentavam e me tentavam a cometer traição, já que eu não podia deixar de comparar o que via em duas dimensões com o que realmente era quando visto em três, e mal conseguia evitar fazer minhas comparações em voz alta. Deixei de lado meus clientes e meus negócios para me dedicar à contemplação dos mistérios que eu havia conhecido, e que, no entanto, não podia transmitir a ninguém, e que achava a cada dia mais difícil de reproduzir mesmo em minha própria mente. (Abbott 2002:74 [122-3])
Finalmente, para completar uma série de indiscrições menores, em uma reunião da Sociedade Especulativa local, que aconteceu no palácio do próprio governador – em que algumas pessoas extremamente tolas haviam lido um artigo rebuscado que dava as razões precisas de a providência ter limitado o número de dimensões a dois, e da onividência ser um atributo apenas do Supremo -, eu me esqueci de mim mesmo de tal modo que dei um relato detalhado de minha viagem com a esfera até o espaço e até a Assembléia Legislativa de nossa metrópole, da volta para o espaço novamente, de meu retorno para casa, e de tudo o que tinha visto e ouvido de fato e em visão. A princípio, fingi estar descrevendo experiências imaginárias de uma pessoa fictícia, mas meu entusiasmo logo me forçou a dispensar o disfarce e, finalmente, em um discurso inflamado, exortei todos os meus ouvintes a se despirem dos preconceitos e se tornarem adeptos da Terceira Dimensão. […] Preciso dizer que fui imediatamente detido e levado perante o Conselho? (Abbott 2002:75 [123-4])
Depois que concluí minha defesa, o presidente, talvez percebendo que alguns dos círculos juniores tinham ficado comovidos com minha evidente veemência, fez duas colocações: […] 1. Se eu poderia indicar a direção a que me referia quando usava a expressão “para cima, e não para o norte”. […] 2. Se eu poderia, por meio de diagramas ou descrições (que não a enumeração de lados e ângulos imaginários), indicar a figura que eu chamava de cubo. […] Declarei que não poderia falar mais nada, e que eu teria de me ater à verdade, cuja causa certamente prevaleceria no final. (Abbott 2002:75 [124])
Daí que estou totalmente desprovido de discípulos, e, por tudo que eu posso ver, a revelação do milênio me foi feita para nada. (Abbott 2002:76 [125])
Às vezes pesa-me a incômoda reflexão de que não posso honestamente dizer que estou seguro do formato exato do cubo visto uma vez – e tantas vezes lamentado -, e em minhas visões noturnas, o misterioso preceito “para cima, e não para o norte” me assombra como uma esfinge devoradora de almas. Faz parte do martírio que sofro pela causa da verdade, que haja períodos de fraqueza mental, quando cubos e esferas passam rapidamente para o pano de fundo de existências quase impossíveis, quando a Terra das Três Dimensões parece quase tão visionária quanto a Terra de Uma ou de Nenhuma. Sim, quando até esta parede dura que me separa de minha liberdade, as mesmas tabuinhas sobre as quais escrevo, e todas as realidades substanciais da própria Planolândia não me parecem melhores do que os produtos de uma imaginação doentia, ou a trama infundada de um sonho. (Abbott 2002:76 [125-6])






 O LaSPA é sediado no Instituto de Filosofia e Ciências Humanas (
O LaSPA é sediado no Instituto de Filosofia e Ciências Humanas (